이번에 컴비 시험을 볼게 생겨서... 시험 전에 전반적인 비전 내용을 쭉 훑어 보고자 합니다.
내용은 매우 간략화 되어 있어 자세한 내용을 알고 싶으시다면 추가적인 자료를 찾아보셔야할 것입니다.
글 마지막에 제가 참고하면서 정리했던 자료들의 링크를 레퍼런스로 남겨두었습니다.
Homogeneous
Homogeneous는 간단하게 (x, y) 좌표를 (x, y, 1) 로 표현한 것이라 볼 수 있습니다.
일반적으로는 (wx, wy, w)로 표현한 것이고 Homogeneous 좌표계에서는 scale 값이 무시 됩니다. 또한 (x, y)에 대한 Homogeneous 좌표는 무수히 많이 표현될 수 있습니다.
Homogeneous 좌표계를 사용하는 이유는 Affine transform이나 perspective transform을 하나의 단일 행렬로 표현하기 위함입니다.
Homography
Homography는 평면 위의 점들이 다른 평면으로 어떻게 변환되는지 기하학적 관계를 정의한다.
즉 서로 다른 두 시점에서 촬영된 이미지 A, B가 있을때 두 이미지의 매칭점들을 통해 두 이미지의 기하학적 관계를 homography로 표현할 수 있다.
Homography는 3x3 행렬로 4쌍 이상의 매칭점들의 좌표를 알아야 구할 수 있다.
RANSAC
RANSAC 알고리즘은 데이터 포인트의 랜덤 샘플을 반복적으로 선택하여 모델을 추정하고, 데이터 분포를 가장 잘 설명하는 데이터를 뽑아 모델을 설정하는 robust한 방법이다.
그럼 RANSAC 알고리즘은 데이터 샘플링을 몇 번 (N) 진행해야할까?
모델을 가장 잘 설명하는 데이터는 최소한 inlier 데이터 일 것이다.
모든 샘플 데이터가 inlier일 확률을 구하면서 RANSAC 알고리즘을 몇 번 (N) 반복할 것인지 구할 수 있다.
p: N번 중 적어도 한번 inlier에서만 샘플이 뽑힐 확률
N: RANSAC의 반복회수
m: 한번에 뽑는 샘플 개수
$a$: 입력 데이터들 중 inlier의 비율
$ p = 1 - (1 - a^{m})^N $
$ N = \frac{\log(1 - p)}{\log(1 - a^{m})} $
Homography estimation을 위한 RANSAC 알고리즘 활용
- 4개의 feature pair를 선택한다.
- 앞서 선택한 feature pair들로 Homography를 계산한다.
- 2에서 추정한 Homography를 활용하여 이미지 1의 feature들을 이미지 2로 투영한 후 매칭쌍들의 차이(residual)를 구한다.
- residual 값들의 SSE (Sum of Squared Error)값을 구하고 기존의 모델보다 낮을 경우 모델을 업데이트한다.
- 1-4 방법을 N번 반복한다.
Canny Edge Detection
Edge detection으로 유명한 알고리즘입니다.
1. 노이즈 제거: 가우시안 필터를 이용해 이미지의 노이즈를 줄여준다
2. 수평, 수직 방향으로 각각 sobel 필터를 적용한 후 gradient를 추출한다.
3. Non-Maximum Suppression: Gradient 크기가 local maximum인 픽셀만을 edge 픽셀로 설정
4. Thresholding, connected edge preserving: 임계값을 2개(MinVal, MaxVal)를 사용하여 강한 엣지는 표시, 약한 엣지는 강한 엣지와 연결될 경우만 표시
Hough Transform
기본적으로 Hough 변환은 이미지 공간에서의 점들을 파라미터 공간(Hough Space)으로 변환하는 과정입니다.
자세히는 $ x, y $ 평면 도메인을 $ \rho, \theta $ 평면 도메인으로 변환하는 작업을 의미합니다.
$ x, y $ 평면 도메인 대신 $ \rho, \theta $ 평면 도메인을 사용하는 이유는 $ y = ax + b $ 식 으로는 수직선 표현이 불가능하다. 반면 $ \rho = xcos\theta + ysin\theta $ 형태는 어떤 기울기의 직선도 표현할 수 있다.
$\rho$: 원점에서 직선까지의 수직거리
$\theta$: 타겟 직선과 수직을 이루는 직선의 각도
$ \rho, \theta $ 평면 도메인의 특징
- 점 $ (x, y) $를 지나는 직선이 회전할 경우 $ \rho, \theta $ 평면 도메인에서 $sin$함수 형상을 갖는다.
- $ \rho, \theta $ 평면 도메인에서의 교점은 $ x, y $ 평면 도메인에서 동일한 한 직선을 표현한다. 즉 같은 기울기와 y절편을 같는다는 의미.
Hough Transform을 이용한 직선 검출 알고리즘
1. Canny Edge 알고리즘 등을 사용하여 영상의 edge를 검출한 후 edge에 해당되는 픽셀 $(x, y)$ 을 선택한다.
2. Hough Space $(\rho, \theta)$를 정의한 후, 이 공간을 작은 cell로 나눈다.
3. edge에 해당되는 픽셀들을 Hough Space에 투영했을때 해당되는 cell에 가중치를 부여한다. (voting)
4. Hough Space에서 가중치가 높은 cell, 즉 많은 엣지 픽셀이 선택한 cell은 실제 이미지 공간에서 직선의 파라미터로 활용된다.
Harris Corner Detector
코너를 검출하는 알고리즘
1) 이미지의 한 픽셀을 중심으로 window를 설정해, window 내의 픽셀값의 합을 $I(x, y)$로 설정한다.
2) 그 후 Window를 x축의 방향으로 u만큼, y축 방향으로 v만큼 이동시키며 $I(x + u, y + v)를 구한다.
3) 여기서 window가 슬라이딩하며 변화한 픽셀값을 계산해 주어야 한다.는데 이 값을 구하는 식은 테일러 전개에 의해 간단한 행렬 곱으로 나타낼 수 있다.
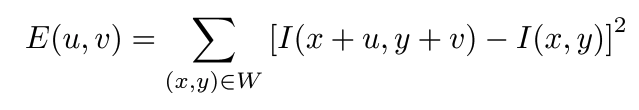
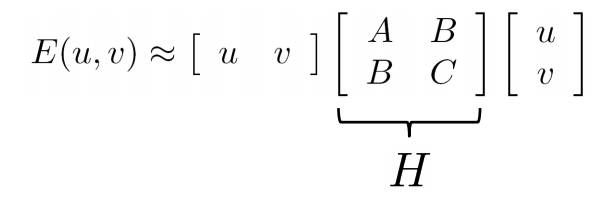
테일러 급수를 활용하여 저렇게 행렬곱으로 나타낼 수 있고 H(2x2) 행렬을 고유값 분해하면, x, y 축 중에 어느 방향으로 이미지 변화가 큰지 알 수 있다.
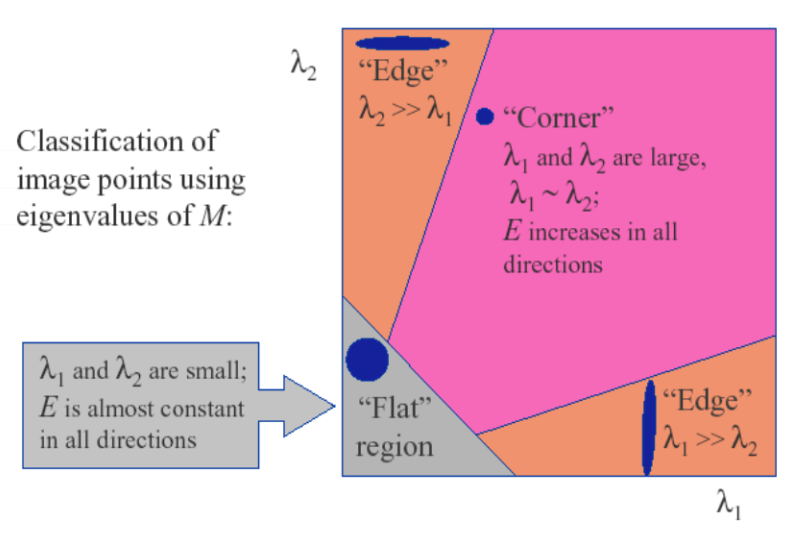
하지만 eigen value를 직접 계산하는 것은 복잡하기 때문에 아래와 같은 공식을 이용해 판별한다.
$R=det(H)−k(trace(H))^2$
1) R > 0 : corner
2) R < 0 : edge
3) R ≈ 0 : flat
($k$는 실험적으로 결정되는 상수로, 일반적으로 0.04에서 0.06 사이의 값을 사용한다고 함.)
Epipolar Geometry
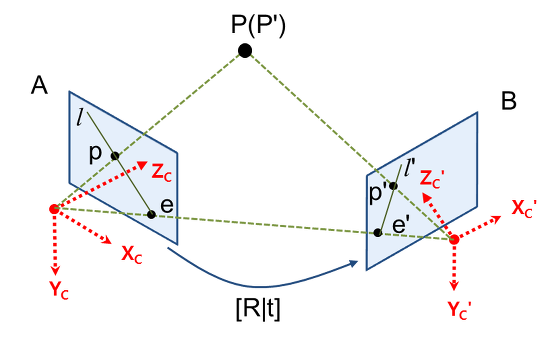
Epipolar Geometry는 동일한 사물 또는 장면에 대해 서로 다른 지점에서 촬영된 영상 A, B를 획들했을때, 영상 A와 영상 B의 매칭쌍들의 기하학적 관계를 다루는 것이다.
epipole: 두 카메라 원점을 잇는 선과 이미지 평면이 만나는 점 e, e'
epipolar line (epiline): 투영점과 epipole을 잇는 직선 l, l'
epipolar plane: 3차원의 점 P와 두 카메라 원점을 잇는 평면
서로 다른 두 시점에서 찍은 영상좌표들 사이에는 Fundamental matrix, Essential Matrix를 매개로 하는 어떤 변환 관계가 성립한다.
Essential Matrix
Essential Matrix는 정규화된 두 이미지의 매칭쌍의 기하학적 관계를 나타내는 행렬이다.
임의의 두 지점 p와 p' 사이에는 아래의 식을 통해 관계지을 수 있으며, 이를 epipolar constraint라고 한다.
$$\mathrm{p}^{\prime T} E \mathrm{p}=0$$
$$\left[\begin{array}{lll}u^{\prime} & v^{\prime} & 1\end{array}\right] E\left[\begin{array}{l}u \\ v \\ 1\end{array}\right]=0$$
Fundamental Matrix
Essential Matrix는 정규화된 이미지에 대한 매칭쌍 사이의 기하학적 관계라 하면 Fundamental Matrix는 카메라 파라미터까지 포함한 두 이미지의 실제 픽셀 좌표 사이의 기하학적 관계를 표현하는 행렬이다.
$$E=K^{\prime T} F K$$
Stereo Camera Calibration
카메라가 가지고 있는 파라미터를 추정하는 방법.
3D-2D의 correspondence를 알고있는 페어가 있어야한다.
즉 아래의 수식에서 이미지 좌표 u, v와 월드 좌표 x, y, z 값을 이미 알고 있는 페어가 몇개 있어야하는 것이다.
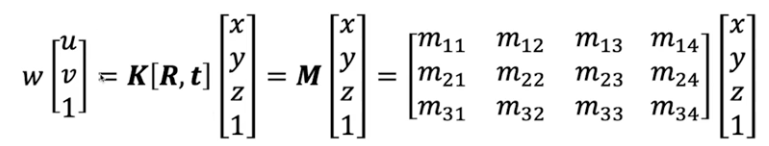
3x4 핼렬은 M은 11 DoF를 가지고 있기 때문에 이를 풀기 위해서는 최소 6쌍의 페어가 있어야 한다.
보통 6쌍의 페어만으로는 정확한 카메라 파라미터를 구하기 어렵기 때문에 보다 많은 페어를 가지고 최적화를 통해 문제를 해결한다.
SIFT (Scale-Invariant-Feature Transform)
크게 과정은 다음과 같다.
1)
Scale Space 구하기 (점진적인 가우시안 필터를 적용하여 이미지를 생성한다.)
Feature의 성질은 scale이 변해도 동일해야한다.
Scale invarient한 feature를 추출하기 위해서 Gaussian filter를 사용하여 이미지를 blur 처리 한다.
(이 blur처리는 멀어질수록 멀어질수록 흐려보이는 특징을 묘사함. 즉 다른 가중치의 가우시안를 사용하여 여러 scale의 이미지를 생성할 수 있음)
DOG (Difference of Gaoussian)
가우시안 필터링된 여러 이미지들에서 인접한 두개의 이미지들끼리 빼주어 DOG 이미지를 얻는다.
(LOG는 연산이 오래걸려 DOG를 대신 사용함)
Keypoint 찾기 (극소값 / 극대값)
연속된 3장의 DOG 이미지를 사용하고 중앙의 한 픽셀에 대해 이웃한 26개의 픽셀중 값이 가장 작거나 큰 경우 극점으로 표시한다.
(2차 Tayler 전개를 사용하여 더 정확한 극값을 찾음)
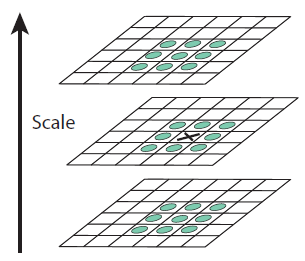
Bad Keypoint 제거
threshold 값을 정해 뽑힌 극점들 중 contrast가 너무 낮거나 edge라서 뽑힌 keypoint들을 제거하고 corner에 위치한 keypoint만 남긴다.
Keypoint orientation 할당
rotation에도 Robust한 특징을 추출하기 위해 keypoint가 어떤 방향으로 되어있는지 정해줘야함.
Keypoint를 중심으로 16x16 윈도우를 생성하여 가우시안 블러링을 해준다.
윈도우 내의 모든 픽셀들의 gradient magnitude와 gradient orientation을 계산한다.
36개의 bin을 가진 orientation histogram 중 가장 높은 값을 갖는 bin을 해당 Keypoint 방향으로 설정
(bin: 방향 히스토그램에서 각도 범위를 나누는 구간 (10도씩의 각도를 담당하면 36개의 bin으로 표현됨))
rotation invariance하게 하기 위해 상대적인 방향 값을 구해야 한다.
기존 16x16의 윈도우를 4x4로 구성하여 16개의 각 윈도우에 속한 픽셀들의 gradient magnitude와 gradient orientation을 구하여 8 bin의 orientation histogram을 생성한다.
앞에서 구한 keypoint 방향에서 16개의 윈도우 각각의 값을 빼서 상대적인 값으로 저장한다.
Optical Flow
시간에 따른 픽셀의 움직임을 추적하여, 객체의 속도와 방향을 파악하는 기법.
일반적으로 연속된 Frame이 들어올때, 영상은 일관성(coherence)의 성질을 가진다.
1) 어떤 픽셀 (x, y)의 색과 그 주변 픽셀들은 서로 비슷한 방향과 속도로 움직일 것이다.
2) 어떤 t 순간의 픽셀 값 $f(y, x, t)$는 다음 순간 $f(y, x, t+1)$과 유사할 가능성이 높다.
3) 연속된 두 프레임 사이의 움직임이 작다.
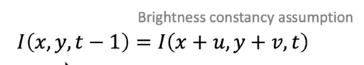
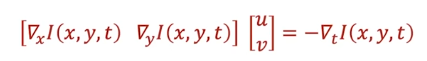
optical flow에서는 $(u, v)$의 값을 얻기 위해 local window를 사용하여 주변 값들이 어떻게 이동하는지 정보를 얻는다.
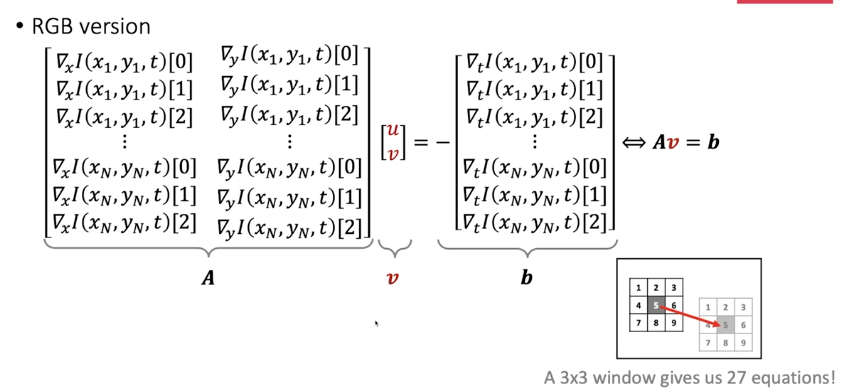
3x3 window를 사용한다고 가정하면 RGB 값을 모두 사용하여 총 27개의 식을 얻을 수 있다.
Lukas-Kanade Flow
unknown보다 eqation의 수가 더 많을 때 해를 구하는 방식.
$u, v$는 결국 다음 프레임에서 이동된 위치를 나타낸다.
추가 자료
SVM
Margin을 극대화하는 최적의 hyper plane을 선택하는 머신러닝 모델이다.
Support Vectors: 결정 경계에 가까이 있는 데이터 포인트들
Margin: 결정 경계와 support vector 사이의 거리로, SVM에서는 이 마진을 최대화하는 결정 경계를 찾는다.
Kernel: 선형적으로 분리가 불가능한 데이터에 대해, 데이터를 고차원 공간으로 매핑하여 선형적으로 분리가 가능하도록 돕는 함수.
모델 학습:
1. margin이 최대가 되는 hyper plane을 선택
2. 결정 경계를 기반으로, 새로운 데이터 포인트가 어느 클래스에 속하는지 분류한다.
3. 잘못된 판단에 패널티를 부여하여 SVM 손실함수 조정.
4. 선형 불가능한 데이터의 경우 kernel을 사용하여 선형 분리 가능한 고차원으로 공간으로 매핑하여 선형적 분리가 가능하도록 함. (kernel trick)
장점:
비선형 데이터를 커널트릭을 이용하여 분류 가능.
고차원의 공간에서 잘 작동함
단점:
대용량의 데이터 처리에는 많은 시간이 소요됨
(업데이트 중...)
[Reference]
Hough Transfom:
https://fwanggu-lee.tistory.com/25
Harris Corner Detector:
https://velog.io/@kowoonho/Harris-Corner-Detection
SIFT:
https://velog.io/@everyman123/SIFT-%EC%95%8C%EA%B3%A0%EB%A6%AC%EC%A6%98-%EC%9D%B4%ED%95%B4%ED%95%98%EA%B8%B0
https://intuitive-robotics.tistory.com/93
https://velog.io/@kowoonho/SIFT-%EC%95%8C%EA%B3%A0%EB%A6%AC%EC%A6%98
https://ballentain.tistory.com/47
Epipolar Geometry:
https://darkpgmr.tistory.com/83